N Queens Problem

                        By  Alex Zhang    

1.n 皇后问题的，distinct solution (可行解)!

n		a(n)
1		1
2		0
3		0
4		2
5		10
6		4
7		40
8		92
9		352
10		724
11		2680
12		14200
13		73712
14		365596
15		2279184
16		14772512
17		95815104
18		666090624
19		4968057848
20		39029188884
21		314666222712
22		2691008701644
23		24233937684440
24		227514171973736
25		2207893435808352
26		22317699616364044

2.我的代码测试 时间！

N=15 -> 2279184

real 0m5.415s

user 0m5.384s

sys 0m0.008s

N=16 -> 14772512

real 0m35.998s

user 0m35.742s

sys 0m0.064s

N=17 -> 95815104

real 4m14.104s

user 4m11.572s

sys 0m0.448s

在下去时间越来越长了......

我怎么到17就这么长了？

你能算到29，，，很强大 。29时有多少可行解?感觉一般算到26就已经是海量时间了，哈哈！

3.别人的一张计算时间，很无敌！                                  有关unique solution   ,看下面.-alex zhang 12/28/09 7:27 PM 

 

4.算法执行步。

从算法执行步来看  ，你的从29 到30  ，跳跃很大啊！

5. unique solution  of n queen problems

通过对称，翻转 ［ symmetry operations (rotations and reflections)］相同的可以看成一个 unique solution .书上的4皇后 对称 看成一个  唯一解。

 6.算法 问题。

我上面使用的是 回溯法，加上递归 调用,树的深度搜索。很平常的方法，

我查了一下改进的方法，

• 使用迭代
• 使用约束编程

7.数学研究，

Velucchi 推导了相关公式，牛！

 k queens on n  chessboard

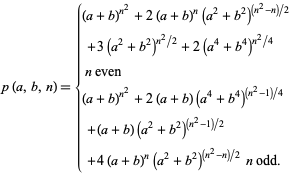
8.代码  ！！

• 递归代码 ，书上的思想！
• #include <stdio.h>
  
  
  int  SIZE, MASK, COUNT;
  
  
  void Backtrack(int y, int left, int down, int right)
  {
      int  bitmap, bit;
  
  
      if (y == SIZE) {
          COUNT++;
      } else {
          bitmap = MASK & ~(left | down | right);
          while (bitmap) {
              bit = -bitmap & bitmap;
              bitmap ^= bit;
              Backtrack(y+1, (left | bit)<<1, down | bit, (right | bit)>>1);
          }
      }
  }
  int main(void)
  {
      SIZE = 17;   /*  <- N  */
      COUNT = 0;   /* result */
  
  
      MASK = (1 << SIZE) - 1;
      Backtrack(0, 0, 0, 0);
  
  
      printf("N=%d -> %d\n", SIZE, COUNT);
      return 0;
  }

• 约束编程思想 ，别人的代码！         //$sudo apt-get install swi-prolog            ;使用 Prolog 语言 。 
• /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
     N Queens animation.
  
  
     Written Feb. 2008 by Markus Triska (triska@gmx.at)
     Public domain code.
  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
  
  
  :- use_module(library(clpfd)).
  
  
  /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
     Constraint posting.
  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
  
  
  n_queens(N, Qs) :-
          length(Qs, N),
          Qs ins 1..N,
          safe_queens(Qs).
  
  
  safe_queens([]).
  safe_queens([Q|Qs]) :- safe_queens(Qs, Q, 1), safe_queens(Qs).
  
  
  safe_queens([], _, _).
  safe_queens([Q|Qs], Q0, D0) :-
          Q0 #\= Q,
          abs(Q0 - Q) #\= D0,
          D1 #= D0 + 1,
          safe_queens(Qs, Q0, D1).
  
  
  
  
  /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
     Animation.
  
  
     For each N of the domain of queen Q, a reified constraint of the form
  
  
        Q #= N #<==> B
  
  
     is posted. When N vanishes from the domain, B becomes 0. A frozen
     goal then emits PostScript instructions for graying out the field.
     When B becomes 1, the frozen goal emits instructions for placing
     the queen. On backtracking, the field is cleared.
  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
  
  
  animate(Qs) :- animate(Qs, Qs, 1).
  
  
  animate([], _, _).
  animate([_|Rest], Qs, N) :-
          animate_(Qs, 1, N),
          N1 #= N + 1,
          animate(Rest, Qs, N1).
  
  
  animate_([], _, _).
  animate_([Q|Qs], C, N) :-
          freeze(B, queen_value_truth(C,N,B)),
          Q #= N #<==> B,
          C1 #= C + 1,
          animate_(Qs, C1, N).
  
  
  queen_value_truth(Q, N, 1) :- format("~w ~w q\n", [Q,N]).
  queen_value_truth(Q, N, 0) :- format("~w ~w i\n", [Q,N]).
  queen_value_truth(Q, N, _) :- format("~w ~w c\n", [Q,N]), false.
  
  
  
  
  /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
     PostScript definitions.
  
  
     Sample instructions, with these definitions loaded:
  
  
     2 init   % initialize a 2x2 board
     1 1 q    % place a queen on 1-1
     1 2 q
     1 2 c    % remove the queen from 1-2
     2 2 i    % gray out 2-2
  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
  
  
  postscript -->
      "/init { /N exch def 340 N div dup scale -1 -1 translate \
               /Palatino-Roman 0.8 selectfont 0 setlinewidth \
               1 1 N { 1 1 N { 1 index c } for pop } for } bind def \
       /r { translate 0 0 1 1 4 copy rectfill 0 setgray rectstroke } bind def \
       /i { gsave 0.5 setgray r grestore } bind def \
       /q { gsave r 0.5 0.28 translate (Q) dup stringwidth pop -2 div 0 moveto \
            1 setgray show grestore } bind def \
       /c { gsave 1 setgray r grestore } bind def\n".
  
  
  /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
     Communication with gs.
  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - */
  
  
  show(N, Options, Qs) :-
          N #> 0,
          open(pipe('gs -dNOPROMPT -g680x680 -dGraphicsAlphaBits=2 -r144 -q'),
               write, Out, [buffer(false)]),
          tell(Out),
          phrase(postscript, Ps),
          n_queens(N, Qs),
          format("~s gsave ~w init\n", [Ps,N]),
          call_cleanup((animate(Qs),labeling(Options, Qs)), close(Out)).
  
  
  
  
  %?- show(N, [ff], Qs).
  
  
  %?- show(8, [ff], Qs).
  %@ Qs = [1, 5, 8, 6, 3, 7, 2, 4] .
  
  
  
  

            测试，

            $swipl -f code.pl

            ?- show(30,[ff,down],Qs).

            Qs = [30, 28, 26, 7, 5, 27, 8, 24, 3|...] .

            测试 30皇后，大概 1s 就出结果了！强大 ！

        对于 60皇后 大概 9s 左右！  

• 迭代思想 ，使用J语言 ，别人的代码 ，很不错！
• queens=: 3 : 0
  z=.i.n,*n=.y.
  for. }.z do.
  b=. -. (i.n) e."1 ,. z +"1 _ ((-i.){:$z) */ _1 0 1
  z=. ((+/"1 b)#z),.(,b)#(*/$b)$i.n
  end.
  )

9.相关 论文 .

N – Queen Problem in Cell:

The n-Queens Problem

On the modular n-queen problem in higher dimensions